Procedural Cave Generation

Level Generation

The key to level generation for Slappy is to assume that they player is not stranded in a wasteland ala the Fallout series, but the player is stranded in an abandoned part of the world. Around him are forests, open space, and enemies trying to kill him. In my head I imagine it being very similar to the movie/book I Am Legend but with our hero choosing to survive in the woods rather than a major metropolitan area.

Each level will be rectangular in nature (easier to model with a computer) and the focus of this blog post is how I have decided to fill in the rectangular area with empty and filled space. The goal of level generation is to create an environment that feels natural and spacious.

Initial Research

Searching for “procedurally generated levels” on Google yields plenty of resources and tutorials. A large portion of these resources are similar to this one: Create a Procedurally Generated Dungeon Cave System. These tend to generate maps that feel like they were designed on graph paper. Whenever I see these I think back to my time playing Dungeons and Dragons with pen and paper. Lately, a lot of these levels have been associated with the rogue-like sub-genre within RPG/Action games.

The tutorials that caught my eye were ones discussing cave generation and were not focused on rougue-like. I would see images like this one:

Looking at that image I can see the top down view of a level that provides freedom to explore the level as the player sees fit, and more importantly it is a level that I would easily believe could occur naturally.

Many of the “procedural cave generation” articles that I read all referenced Cellular Automata and one algorithm in particular Cellular Automata Method for Generating Random Cave-Like Levels. I am not sure who is the first to discover this particular cellular automata, nor who was the first to apply it to procedural cave generation, but I will try to call out each of the interesting articles that helped me refine my level generator.

Initial Implementation

I have written a simple libGDX application for exploring different procedural generation algorithms that can be found on my GitHub account. Each blog post will have a tag so that you can download the specific version of the code that I’m referring to, since I plan to continually update the code.

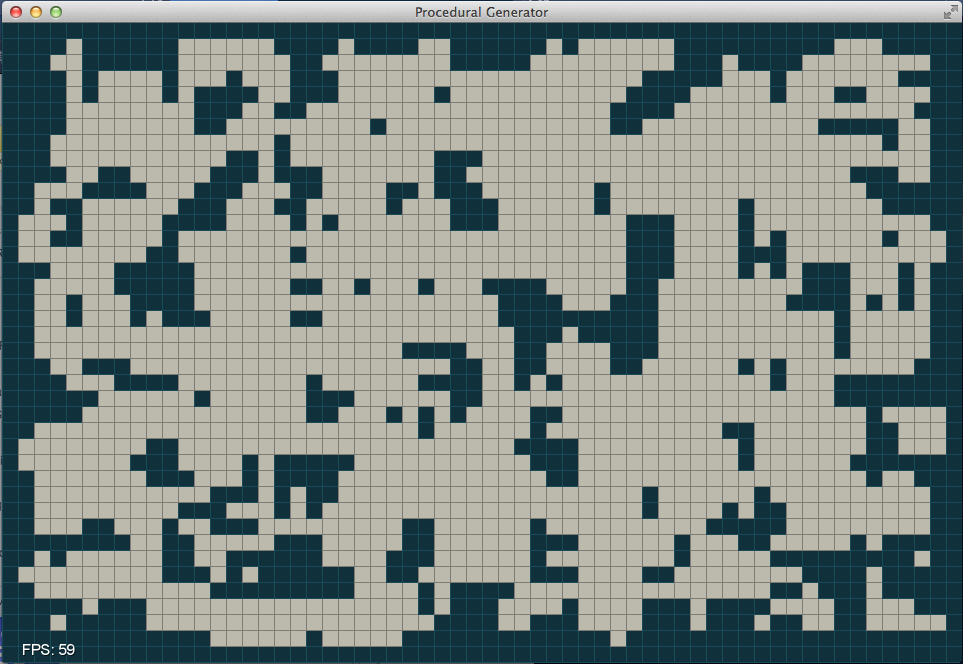
The cave generation algorithm is based on a cellular automata (Wikipedia). The level is represented as a two-dimensional matrix (boolean[][]) and each cell can be in one of two states (EMPTY or FILLED). The matrix is initialized randomly with roughly 40% of the matrix starting out filled. The borders of the matrix are also initialized as filled just to ensure that the player is unable to walk off of the map. A sample initialized matrix is visualized below.

Now that our matrix is initialized we can begin evolving the cave structure by repeatedly applying some rules for deciding whether or not a cell stays filled or becomes empty. The rules are applied to each cell in the matrix independently. In the cellular automata literature, these rules can also be referred to as a birth rule and a survival rule. There are two inputs to the rules that we define, each one is a count of the number of neighbors within a specified range that are filled. A visual demonstration of the neighborhoods is shown below.

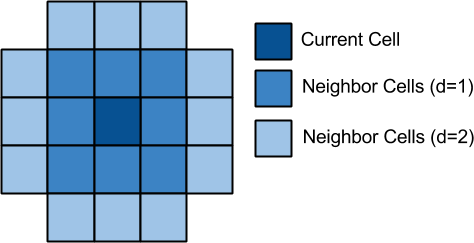
It is important to point out that although it looks like the nieghborhoods are disjoint, d=2 actually contains all of d=1.

The rules that I used are a combination of those found in these two articles: one and two. After initialization there are two phases to our cellular automate. The first of these phases is responsible for carving out the main cave structure, and the second phase refines the structure and clears out some of the middle to create more open spaces.

We define the following rules:

if count(d_1) >= x
  cell = FILLED
else if count(d_2) <= y
  cell = FILLED
else
  cell = EMPTY

In the first phase x=5 and y=2. After one iteration we have the following:

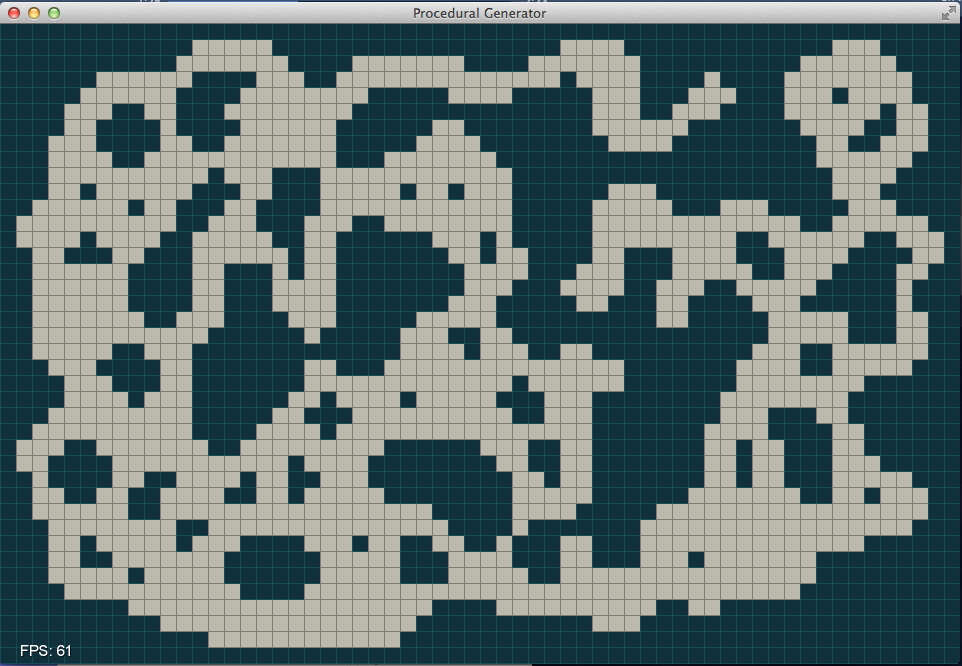
And after a few more iterations we can see the cave structure emerging.

In the second phase we set x=5 and y=-1 effectively shutting down the second conditional since there cannot have a negative number of filled cells around a cell in the matrix. This begins removing small chunks in the middle that do not have enough neighbors to stay around and opens up the space on the interior.

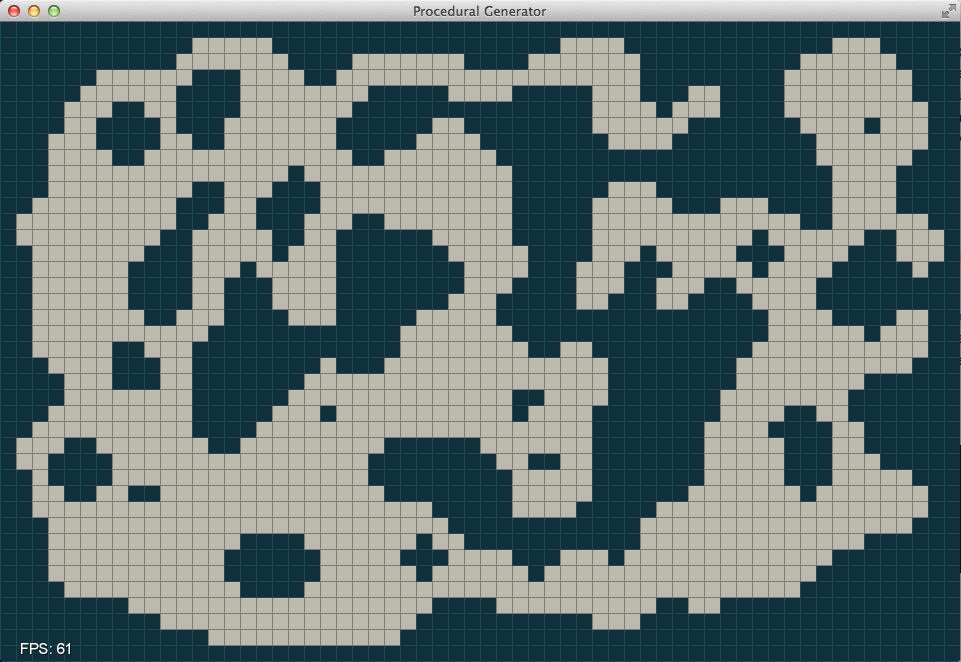
And after a few more iterations.

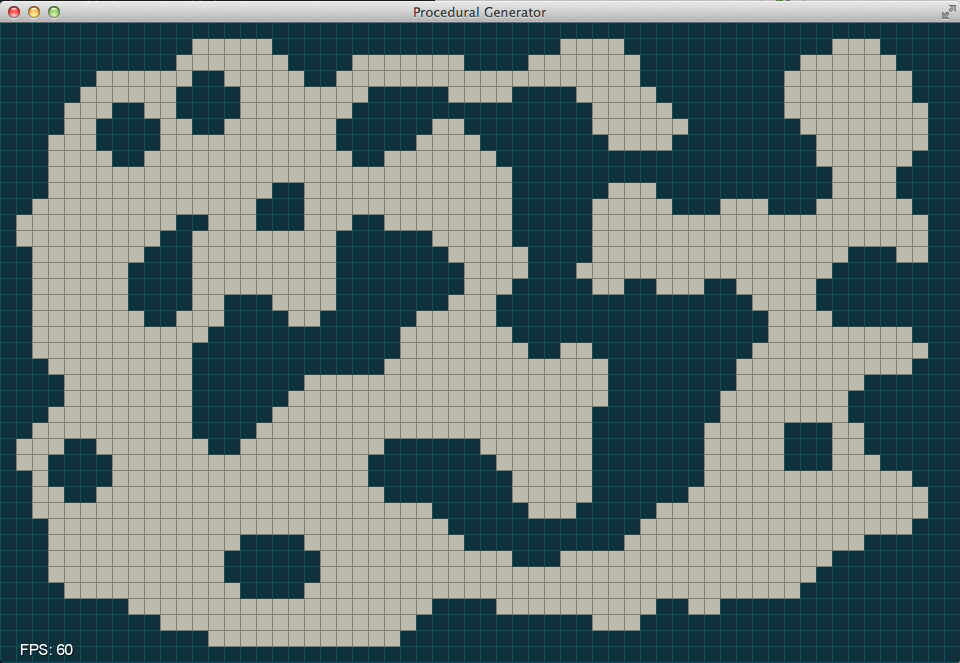
We have now reached a reasonable looking cave and happened to be lucky enough that all of the chambers are connected. There is a small bit of code included with the cave generation code to ensure that all rooms are connected. The basic idea is to use a “flood fill” algorithm to identify all of the unique rooms in the level (redblobgames.com). Once we have identified the unique rooms we begin a random walk towards the center of the map clearing out filled cells until we hit another room.

Running Demo

I included a demo of the system running (thanks to LibGDX HTML5 output).

Thanks for reading this far, and feel free to send me any feedback.